1. k-nearest neighbors algorithms
Nhắc lại từ bài viết trước: mọi bài toán machine learning đều cần được một giả định nào đấy để chọn thuật toán hiệu quả cho nó.
Với thuật toán k-nearest-neighbors (kNN), ta đã đặt ra một giả định rằng: những feature (gần) giống nhau thì có label giống nhau. Với bài toán classification dùng kNN, giả định đó được cụ thể thành: với feature dùng để test
Chính xác hơn, giả sử ta có một tập dữ liệu
Khi đó, hàm
trong đó
Một điểm đáng lưu ý khi sử dụng thuật toán này đó là việc chọn
Để trực quan hơn, mình đã viết ra một demo cho kNN ở đây (cập nhật sau khi hoàn thành).
Ngoài ra, kNN có một số các tính chất toán học khác, mình sẽ để dành ở một bài viết khác.
Metric dùng trong kNN
Metric được sử dụng phổ biến trong kNN chính là Minkowski distance:
Một số trường hợp đặc biệt của
(Manhattan distance)
(Euclidean distance)
(Chebyshev distance)
Chứng minh cho trường hợp
: Ta có đánh giá: Hay:
Để ý
, cho trong đánh giá trên, ta có ngay điều phải chứng minh.
Như vậy, ta đã hiểu khá rõ cách kNN classifier hoạt động.
Ưu nhược điểm:
Ưu điểm của kNN là đơn giản, việc dự đoán kết quả không quá phức tạp và không làm gì ở phần traning data cả. Tuy nhiên nhược điểm chính là mọi tính toán đều nằm ở khâu test, ta cần tính khoảng cách giữa mọi cặp điểm - rất phức tạp khi số dữ liệu và số chiều của dữ liệu lớn. Việc này cũng khiến tốn rất nhiều dung lượng bộ nhớ để lưu dataset (vì khâu test dùng đến cả dataset). Thêm nữa, để chọn cho đúng k cũng là một vấn đề.
Ngoài ra, kNN cũng gặp một vấn đề, là vấn đề chung cho các thuật toán: Curse of Dimensionality.
2. Curse of Dimensionality (đọc thêm)
Phần lớn không gian là rỗng
Nhắc lại về giả định mà ta đặt ra khi dùng kNN: những điểm (gần) giống nhau thì có label như nhau. Cụ thể hơn, thước đo cho sự (gần) giống nhau chính là độ gần, đo bằng metric. Tuy nhiên, khi ở trong một không gian rất nhiều chiều, những điểm trong dataset dường như lại không hề gần nhau.
Để hiểu hơn về curse of dimensionality, ta hãy bắt đầu với 1-d. Không mất tính tổng quát, giả sử ta có các điểm dữ liệu phân bố đều và độc lập, nằm trên đoạn
.png) {: .dark }
{: .dark }
.png) {: .light }
{: .light }
Rõ ràng, xác suất mà điểm dữ liệu đã cho không nằm ở rìa là
Giờ hãy xét ở 2-d, khi đó data của chúng ta là phân bố đều và nằm ở trong
.png) {: .dark }
{: .dark }
.png) {: .light }
{: .light }
Ta thấy một cách trực quan rằng có vẻ như xác suất mà data của chúng ta không nằm ở rìa có vẻ hơi giảm đi. Thật vậy, tỉ lệ phần không bị gạch (rìa) với toàn diện tích hình vuông là
Vậy sẽ như nào nếu số chiều
Sự mất ý nghĩa của khoảng cách
Hệ quả của việc không gian phần lớn là rỗng chính là phần lớn khoảng cách giữa 2 điểm bất kỳ là rất giống nhau (đều là khoảng cách từ đầu này đến đầu kia). {: .prompt-danger }
Để hiểu hệ quả trên một cách trực quan quan hơn, ta lấy ví dụ trong không gian 2 chiều tiếp. Giả sử các điểm dữ liệu của ta đều ở biên và phân bố đều. Lấy 1 điểm màu đỏ nằm ở rìa, rõ ràng quá nửa số data nằm xa điểm màu đỏ (bên ngoài đường tròn đỏ), tức là quá nửa khoảng cách tới điểm đỏ nằm trong khoảng
.png) {: .dark }
{: .dark }
.png) {: .light }
{: .light }
Từ ví dụ 2d này, ta hãy nghĩ rằng khi tăng số chiều lên, hiệu ứng này nó sẽ lớn hơn rất nhiều, là quá nửa số khoảng cách sẽ nằm trong 1 khoảng không gian rất là nhỏ. Như vậy, khi
Ví dụ, bạn ở Hà Nội và 5 người gần nhất với bạn lần lượt ở Hòa Bình, Đà Nẵng và 3 người ở Hồ Chí Minh. Nếu như dùng 5-NN, thì khẳng định rằng bạn giống với 3 người ở HCM là không hợp lý chút nào.
Dưới đây là biểu đồ minh họa cho sự phân bố của các khoảng cách của một tập dữ liệu phân bố đều trong các không gian.
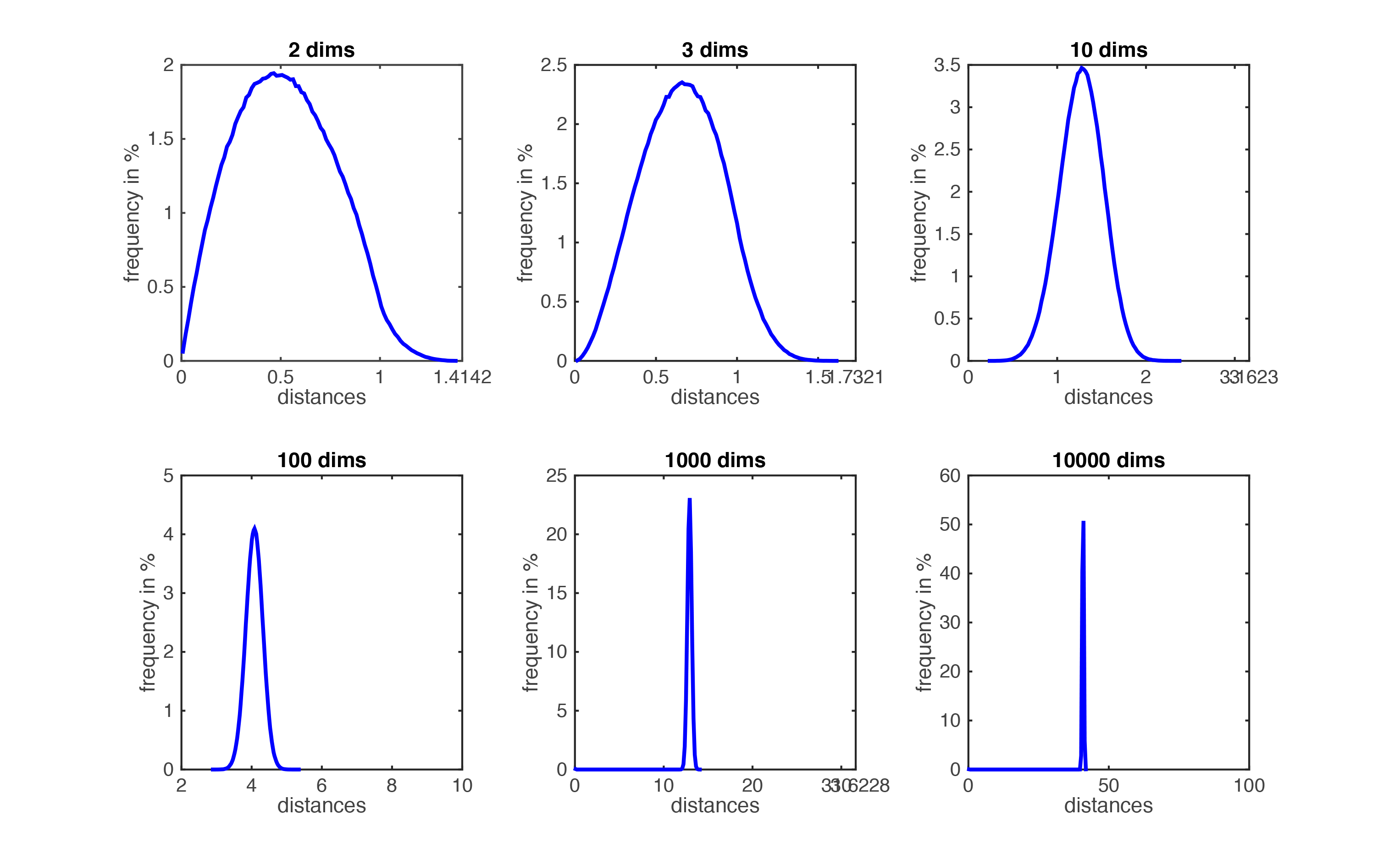 Phân bố khoảng cách giữa 2 cặp điểm khi
Phân bố khoảng cách giữa 2 cặp điểm khi
Chứng minh toán học cho hiện tượng này ở đây: (cập nhật sau khi hoàn thiện).
Như vậy, kNN hoàn toàn không thể ứng dụng trong thực tế ư? Bởi số chiều của data trong thực tế là rất lớn.
Ví dụ như với một tập các hình ảnh hoa oải hương có kích thước 100x100, số chiều của dữ liệu là 30 000 (giả sử mỗi điểm là 1 bộ 3 (r,g,b) ).
Thật ra không phải là không ứng dụng được. Bởi với curse of dimensionality, data là phân bố đều và độc lập. Còn thực tế, data của chúng ta không hề phân bố đều mà nằm trong một mặt phẳng (hoặc là một manifold) có
Manifold là một khái niệm topology, có thể hiểu nôm na là khi ta nhìn cục bộ thì rất giống với không gian
chiều. Ví dụ như chúng ta đang ở Trái Đất, một vật thể 3d. Nhưng chúng ta chỉ di chuyển trên bề mặt Trái Đất và Trái Đất quá lớn so với chúng ta, nên nhìn cục bộ có vẻ như Trái Đất phẳng (2d).
 Ví dụ về data nằm trên một manifold
Ví dụ về data nằm trên một manifold
Lấy lại ví dụ với tập ảnh hoa oải hương, mỗi hoa oải hương đều có cấu trúc tương tự nhau như cánh hoa nhỏ màu tím nằm thành chùm trên cành xanh dài mảnh, tạo cảm giác nhẹ nhàng, cánh đồng oải hương thì tím bạt ngàn,… Vì thế data của chúng ta sẽ nằm trên một manifold nào đó chứ không phân bố ngẫu nhiên được. Do đó kNN vẫn có thể áp dụng được.
Thật ra, một ý tưởng rất hiển nhiên để giải quyết curse of dimensionality chính là tìm cách giảm số chiều xuống. Có nhiều kỹ thuật để làm điều này và sẽ được bàn trong một (vài) bài viết trong tương lai.