1. The black box method
The term comes from this video. I’d thought about this idea long before, but I was too lazy to think it through carefully or actually apply it to my life. Then I happened to see that video on YouTube, and it made me want to write about this method.
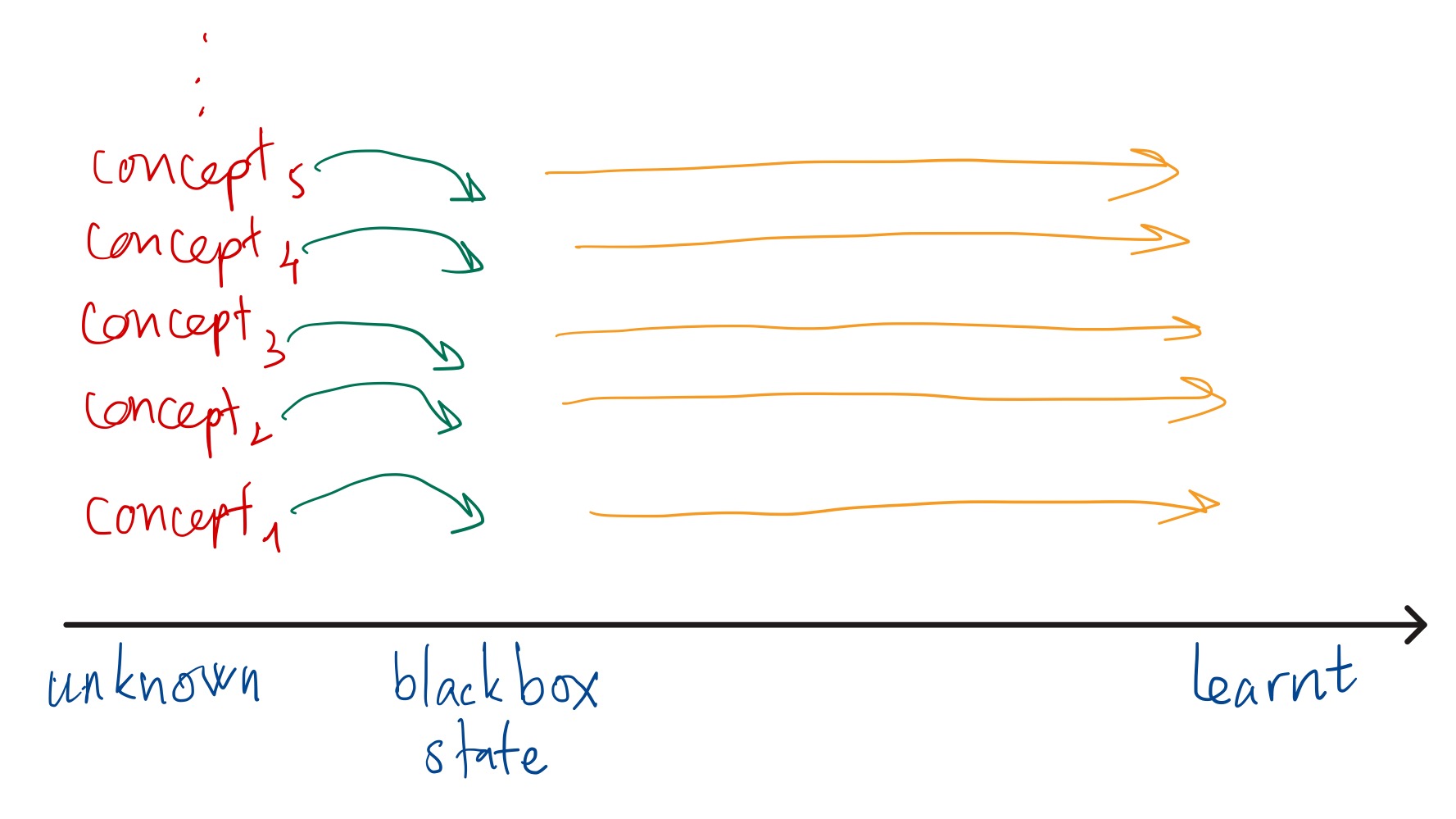
A black box is something whose input and output you know, but you don’t (need to) understand how it works internally. Obviously, learning a black box is much easier than learning the reasoning behind how it works.
Suppose you have some concepts from a book or a specific topic that you want to learn. Fully learning each concept takes a lot of effort and time, especially when there are many of them. The black box method means you don’t learn those concepts one by one, finishing each before moving on. Instead, you first treat them as black boxes: learn what their inputs and outputs are, and how they’re used to solve problems or interact with other concepts. You do this for all of them, staying at the surface level at first. Then, later on, you can dive deeper and fully learn each one.
 Blackbox method
Blackbox method
 Usual method
Usual method
The advantage of this method is that you can grasp the overall view of the book/the topic, which consists of the concepts, in the early stage of the whole process. You can start applying what you’ve learned even before you’ve mastered every detail. And this actually makes the learning process more fun because you can already make or try simple things.
This method doesn’t avoid full learning; it just postpones it. So it seems to have no real downside compared to the usual one-by-one approach. At the time of writing this, I haven’t found any disadvantages. The only condition is that the concepts should be close enough in difficulty and somewhat independent from how the others work internally. That’s why the concepts are ideally from the same book or narrow topic.
2. How I apply it.
2.1 Mathematics
I read the whole textbook, or maybe just a chapter, and learn the definitions and theorems, but not the proofs yet. When I read it the second time, that’s when I read the proof. After that, I try to write all the theorems and prove them (yeah ik that’s kinda cheating since I have read the proofs). Finally, I do the exercises.
There is this math blog web that follows the above order and I really love it.
2.2 Computer Science/AI
This is my major, and the process is similar to math. First, I choose the concepts I want to learn, then go over the key definitions, tools, and problems (from lecture slides or Kaggle). For the problems, I skim through all the solution code. After that, I try to reason why each approach works well. Finally, I do some exercises or a small project.